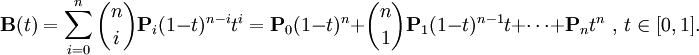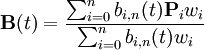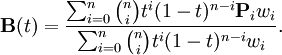Bezier curve
From Wikipedia, the free encyclopedia
In the mathematical field of numerical analysis, a Bezier curve is a parametric curve important in computer graphics. Generalizations of Bezier curves to higher dimensions are called Bezier surfaces, of which the Bezier triangle is a special case.
Bezier curves were widely publicised in 1962 by the French engineer Pierre Bezier, who used them to design automobile bodies. The curves were first developed in 1959 by Paul de Casteljau using de Casteljau's algorithm, a numerically stable method to evaluate Bezier curves.
Contents[hide] |
Examination of cases
Linear Bezier curves
Given points P0 and P1, a linear Bezier curve is just a straight line between those two points. The curve is given by
and is equivalent to linear interpolation.
Quadratic Bezier curves
A quadratic Bezier curve is the path traced by the function B(t), given points P0, P1, and P2,
TrueType fonts use Bezier splines composed of the quadratic Bezier curves.
Cubic Bezier curves
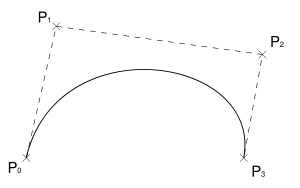
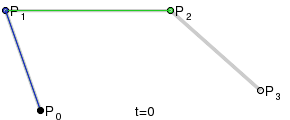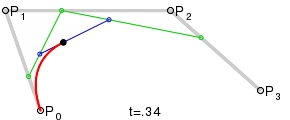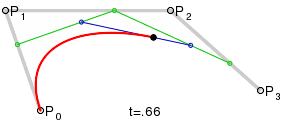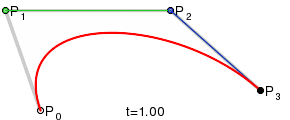
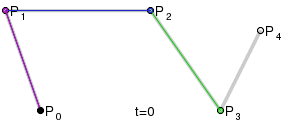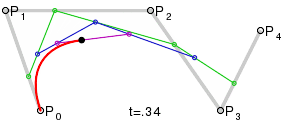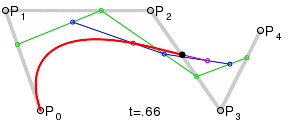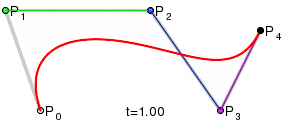
Four points P0, P1, P2 and P3 in the plane or in three-dimensional space define a cubic Bezier curve. The curve starts at P0 going toward P1 and arrives at P3 coming from the direction of P2. Usually, it will not pass through P1 or P2; these points are only there to provide directional information. The distance between P0 and P1 determines "how long" the curve moves into direction P2 before turning towards P3.
The parametric form of the curve is:
Modern imaging systems like PostScript, Asymptote and Metafont use Bezier splines composed of cubic Bezier curves for drawing curved shapes.
Generalization
The Bezier curve of degree n can be generalized as follows. Given points P0, P1,..., Pn, the Bezier curve is
For example, for n = 5:
This formula can be expressed recursively as follows: Let ![]() denote the Bezier curve determined by the points P0, P1,..., Pn. Then
denote the Bezier curve determined by the points P0, P1,..., Pn. Then
In words, the degree n Bezier curve is an interpolation between two degree n ? 1 Bezier curves.
Terminology
Some terminology is associated with these parametric curves. We have
where the polynomials
are known as Bernstein basis polynomials of degree n, defining 00 = 1.
The points Pi are called control points for the Bezier curve. The polygon formed by connecting the Bezier points with lines, starting with P0 and finishing with Pn, is called the Bezier polygon(or control polygon). The convex hull of the Bezier polygon contains the Bezier curve.
Notes
- The curve begins at P0 and ends at Pn; this is the so-called endpoint interpolation property.
- The curve is a straight line if and only if all the control points lie on the curve. Similarly, the Bezier curve is a straight line if and only if the control points are collinear.
- The start (end) of the curve is tangent to the first (last) section of the Bezier polygon.
- A curve can be split at any point into 2 subcurves, or into arbitrarily many subcurves, each of which is also a Bezier curve.
- Some curves that seem simple, such as the circle, cannot be described exactly by a Bezier or piecewise Bezier curve (though a four-piece Bezier curve can approximate a circle, with a maximum radial error of less than one part in a thousand, when each inner control point is the distance
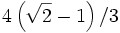 horizontally or vertically from an outer control point on a unit circle).
horizontally or vertically from an outer control point on a unit circle). - The curve at a fixed offset from a given Bezier curve, often called an offset curve (lying "parallel" to the original curve, like the offset between rails in a railroad track), cannot be exactly formed by a Bezier curve (except in some trivial cases). However, there are heuristic methods that usually give an adequate approximation for practical purposes.
Constructing Bezier curves
Linear curves
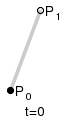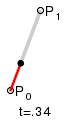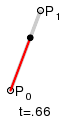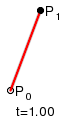
The t in the function for a linear Bezier curve can be thought of as describing how far B(t) is from P0 to P1. For example when t=0.25, B(t) is one quarter of the way from point P0 to P1. As t varies from 0 to 1, B(t) describes a straight line from P0 to P1.
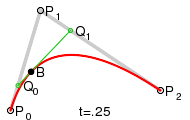
Quadratic curves
For quadratic Bezier curves one can construct intermediate points Q0 and Q1 such that as t varies from 0 to 1:
- Point Q0 varies from P0 to P1 and describes a linear Bezier curve.
- Point Q1 varies from P1 to P2 and describes a linear Bezier curve.
- Point B(t) varies from Q0 to Q1 and describes a quadratic Bezier curve.
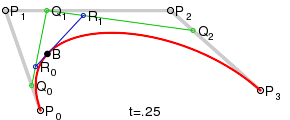
Higher order curves
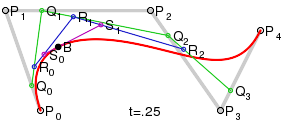
For higher order curves one needs correspondingly more intermediate points. For cubic curves one can construct intermediate points Q0, Q1 & Q2 that describe linear Bezier curves, and points R0 & R1 that describe quadratic Bezier curves:
And for fourth order curves one can construct intermediate points Q0, Q1, Q2 & Q3 that describe linear Bezier curves, points R0, R1 & R2 that describe quadratic Bezier curves, and pointsS0 & S1 that describe cubic Bezier curves:
(See also a construction of a fifth order Bezier curve.)
Applications
Computer graphics
Bezier curves are widely used in computer graphics to model smooth curves. As the curve is completely contained in the convex hull of its control points, the points can be graphically displayed and used to manipulate the curve intuitively. Affine transformations such as translation, scaling and rotation can be applied on the curve by applying the respective transform on the control points of the curve.
Quadratic and cubic Bezier curves are most common; higher degree curves are more expensive to evaluate. When more complex shapes are needed, low order Bezier curves are patched together. To guarantee smoothness, the control point at which two curves meet and one control point on either side must be collinear. This is commonly referred to as a "path" in programs like Adobe Illustrator or Inkscape. These poly-Bezier curves can also be seen in the SVG file format.
The simplest method for scan converting (rasterizing) a Bezier curve is to evaluate it at many closely spaced points and scan convert the approximating sequence of line segments. However, this does not guarantee that the rasterized output looks sufficiently smooth, because the points may be spaced too far apart. Conversely it may generate too many points in areas where the curve is close to linear. A common adaptive method is recursive subdivision, in which a curve's control points are checked to see if the curve approximates a line segment to within a small tolerance. If not, the curve is subdivided parametrically into two segments, ![]() and
and ![]() and the same procedure applied to recursively to each half. There are also forward differencing methods, but great care must be taken to analyse error propagation. Analytical methods where a spline is intersected with each scan line involve finding roots of cubic polynomials (for cubic splines) and dealing with multiple roots, so they are not often used in practice.
and the same procedure applied to recursively to each half. There are also forward differencing methods, but great care must be taken to analyse error propagation. Analytical methods where a spline is intersected with each scan line involve finding roots of cubic polynomials (for cubic splines) and dealing with multiple roots, so they are not often used in practice.
Code example
The following code is a simple practical example showing how to plot a cubic Bezier curve using the C programming language. Note, this simply computes the coefficients of the polynomial and runs through a series of t values from 0 to 1 ? in practice this is not how it is usually done - a recursive solution is often faster, taking fewer processor cycles at the expense of requiring more memory temporarily. However the direct method illustrated here is easier to understand and produces the same result. The following code has been factored to make its operation clear ? an optimization in practice would be to compute the coefficients once and then re-use the result for the actual loop that computes the curve points ? here they are recomputed every time, which is less efficient but helps to clarify the code.
The resulting curve can be plotted by drawing lines between successive points in the curve array ? the more points, the smoother the curve.
On some architectures, the code below can also be optimized by dynamic programming. E.g. since dt is constant, cx * t changes a constant amount with every iteration. By repeatedly applying this optimization, the loop can be rewritten without any multiplications (though such a procedure is not numerically stable).
/*
Code to generate a cubic Bezier curve
*/
typedef struct
{
float x;
float y;
}
Point2D;
/*
cp is a 4 element array where:
cp[0] is the starting point, or P0 in the above diagram
cp[1] is the first control point, or P1 in the above diagram
cp[2] is the second control point, or P2 in the above diagram
cp[3] is the end point, or P3 in the above diagram
t is the parameter value, 0 <= t <= 1
*/
Point2D PointOnCubicBezier( Point2D* cp, float t )
{
float ax, bx, cx;
float ay, by, cy;
float tSquared, tCubed;
Point2D result;
/* calculate the polynomial coefficients */
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/* calculate the curve point at parameter value t */
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
return result;
}
/*
ComputeBezier fills an array of Point2D structs with the curve
points generated from the control points cp. Caller must
allocate sufficient memory for the result, which is
<sizeof(Point2D) numberOfPoints>
*/
void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve ) {
float dt;
int i;
dt = 1.0 / ( numberOfPoints - 1 );
for( i = 0; i < numberOfPoints; i++)
curve[i] = PointOnCubicBezier( cp, i*dt );
}
Another application for Bezier curves is to describe paths for the motion of objects in animations, etc. Here, the x, y positions of the curve are not used to plot the curve but to position a graphic. When used in this fashion, the distance between successive points can become important, and in general these are not spaced equally ? points will cluster more tightly where the control points are close to each other, and spread more widely for more distantly positioned control points. If linear motion speed is required, further processing is needed to spread the resulting points evenly along the desired path.
Rational Bezier curves
The rational Bezier adds adjustable weights to provide closer approximations to arbitrary shapes. The numerator is a weighted Bernstein-form Bezier curve and the denominator is a weighted sum of Bernstein polynomials.
Given n + 1 control points Pi, the rational Bezier curve can be described by:
or simply
See also
- de Casteljau's algorithm
- Spline (mathematics)
- Bezier spline
- Bezier surface
- Bezier triangle
- NURBS
- string art - Bezier curves are also formed by many common forms of string art, where strings are looped across a frame of nails.
- Hermite curve
References
- Paul Bourke: Bezier curves, http://astronomy.swin.edu.au/~pbourke/curves/bezier/
- Donald Knuth: Metafont: the Program, Addison-Wesley 1986, pp. 123-131. Excellent discussion of implementation details; available for free as part of the TeX distribution.
- Dr Thomas Sederberg, BYU Bezier curves, http://www.tsplines.com/resources/class_notes/Bezier_curves.pdf
- J.D. Foley et al.: Computer Graphics: Principles and Practice in C (2nd ed., Addison Wesley, 1992)
External links
- Bezier Curves interactive applet
- 3rd order Bezier Curves applet
- Living Math Bezier applet
- Living Math Bezier applets of different spline types, JAVA programming of splines in An Interactive Introduction to Splines
- Don Lancaster's Cubic Spline Library describes how to approximate a circle (or a circular arc, or a hyperbola) by a Bezier curve; using cubic splines for image interpolation, and an explanation of the math behind these curves.
- Eric W. Weisstein, Bezier Curve at MathWorld.
- Quadratic Bezier Curve Construction - An interactive applet showing how to construct a quadratic Bezier curve geometrically. (Requires Java.)
- Cubic Bezier Curve Construction - An interactive applet showing how to construct a cubic Bezier curve geometrically. (Requires Java.)
- Bezier / Parabola - An interactive applet showing the relationship between the quadratic Bezier curve and the parabola. (Requires Java.)
- PolyBezier - The Microsoft Win32 GDI API function, which draws Bezier curves in Windows graphic applications, like MS Paint.